Density Calculator
Calculate density by entering the mass and volume in the calculator below. Alternatively, solve mass or volume using the density.
Density:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Teresa is a chemistry expert with a PhD in environmental science, a Master's degree in earth, atmospheric, and planetary sciences, and Bachelor's degree in chemistry.
How to Calculate Density
Density is the measure of mass per volume, or essentially how compact or dense a substance or object is. It is expressed as mass per unit volume; for example: g/m3.
Density is expressed using the Greek letter ρ (rho), and you can calculate it using a standard formula.
Density Formula
To calculate the density of a material or substance, divide the mass of an object or substance by its volume.
ρ = m / V
where:
ρ = density (g/L or g/m3)
m = mass (g)
V = volume (L or m3)
The units for density depend on the form of the substance. Solids will be measured in g/m3 or g/cm3, while liquids or gasses will be measured in g/L.
If you know the mass in kilograms, convert to grams by multiplying the value by 1,000 (g = kg × 1,000).
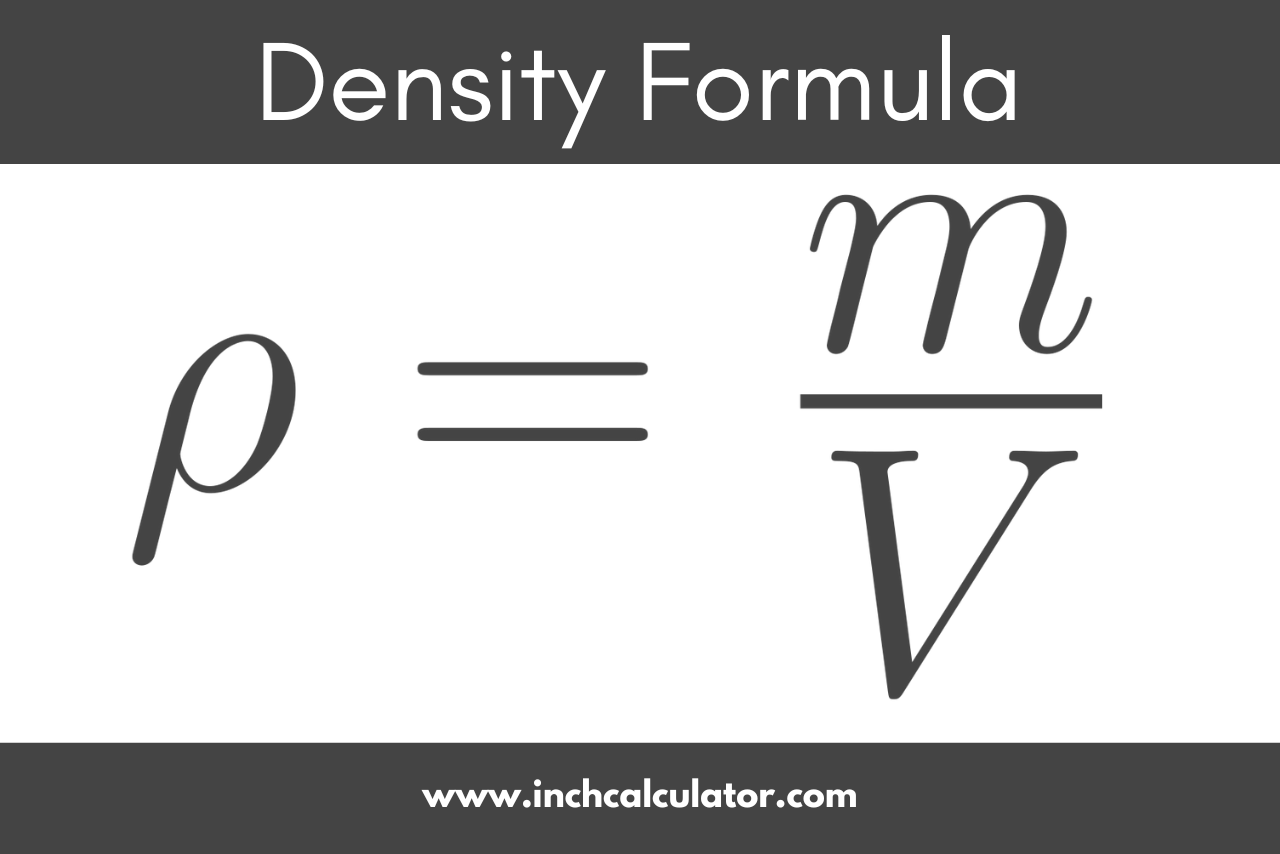
For example, let’s find the density ρ of an object that weighs 5 grams and has a volume of 2 cubic centimeters.
ρ = 5 g ÷ 2 cm3
ρ = 2.5 g/cm3
Tip: for solid objects, you can multiply the length by the width by the height or use our calculator to find the volume.
How to Calculate Density for U.S. Customary Units
The formula above works well for SI units of mass and volume. It’s possible to find the density of an object when the mass and volume are in U.S. customary units of measure.
The key to finding the density in the desired unit of measure is to convert the mass unit and the volume unit to the right measurements before using the formula above.
For example, let’s find the density of an object in pounds per cubic foot for an object that weighs 80 ounces and has a volume of 3,456 cubic inches.
First, convert the mass to pounds.
m(oz) = 80 oz
m(lb) = 80 oz ÷ 16 oz per pound
m(lb) = 5 lbs
Second, convert the volume to cubic feet.
V(in3) = 3,456 in3
V(ft3) = 3,456 in3 ÷ 1,728 in3 per ft3
V(ft3) = 2 ft3
Now that that mass and volume are in the correct output unit, enter them in the formula above to find density.
How to Calculate Mass From Density and Volume
Using the formula above, it’s also possible to calculate the mass if the density and volume are known. We can rearrange the formula above to find the mass.
m = ρ × V
where:
m = mass (g)
ρ = density (g/L or g/m3)
V = volume (L or m3)
For example, let’s find the mass m of an object with a density of 4 g/cm3 and a volume of 3 cm3.
m = 4 g/cm3 × 3 cm3
m = 12 g
Tip: if you aren’t sure what the volume is, use a tool such as our cubic meters or cubic feet calculator to find it.
How to Calculate Volume using Mass and Density
It’s also possible to calculate volume if both mass and density are known. Rewriting the original formula like this will allow solving for volume.
V = m / ρ
where:
V = volume (L or m3)
m = mass (g)
ρ = density (g/L or g/m3)
For example, let’s find the volume V of an object with a density of 2 g/cm3 and a mass of 6 grams.
V = 6 g ÷ 2 g/cm3
V = 3 cm3
Common Material Densities
| Material | Density |
|---|---|
| water (at 4 °C) | 1.0 g/cm³ |
| isopropyl alcohol | 0.786 g/cm³ |
| gasoline | 0.77 g/cm³ |
| milk | 1.026 g/cm³ |
| latex paint | 1.34 g/cm³ |
| aluminum | 2.7 g/cm³ |
| brass | 8.73 g/cm³ |
| copper | 8.96 g/cm³ |
| iron | 7.86 g/cm³ |
| steel | 8.050 g/cm³ |
| platinum | 21.45 g/cm³ |
| air | 0.001225 g/cm³ |
| carbon dioxide | 0.001977 g/cm³ |
| helium | 0.000179 g/cm³ |
You might also find our water weight calculator and hardwood lumber calculator interesting, which use these same principles of density to determine the mass of these materials.