Resistor Capacitor Circuit Calculator
Calculate the charge time, energy, and characteristic frequency or the impedance, reactance, and angular frequency of a resistor-capacitor circuit.
Calculate Energy & Charge Time
Calculate Impedance & Reactance
Results:
| Time Constant | |
|---|---|
| seconds | |
| Energy | |
| joules | |
| Current | |
| amps | |
| Charge | |
| coulombs | |
| Frequency | |
| hertz | |
| Impedance | |
|---|---|
| Ω | |
| Capacitive Reactance | |
| Ω | |
| Phase Difference | |
| degrees | |
| Angular Frequency | |
| rad/s | |
On this page:
A resistor-capacitor circuit, or RC circuit, is a circuit with a resistor and capacitor connected in series. The capacitor in the circuit stores energy and the resistor changes the charge and discharge rate of the capacitor. These circuits are most commonly used for filtering the waveform and are used to create low-pass, high-pass, and band-pass filters.
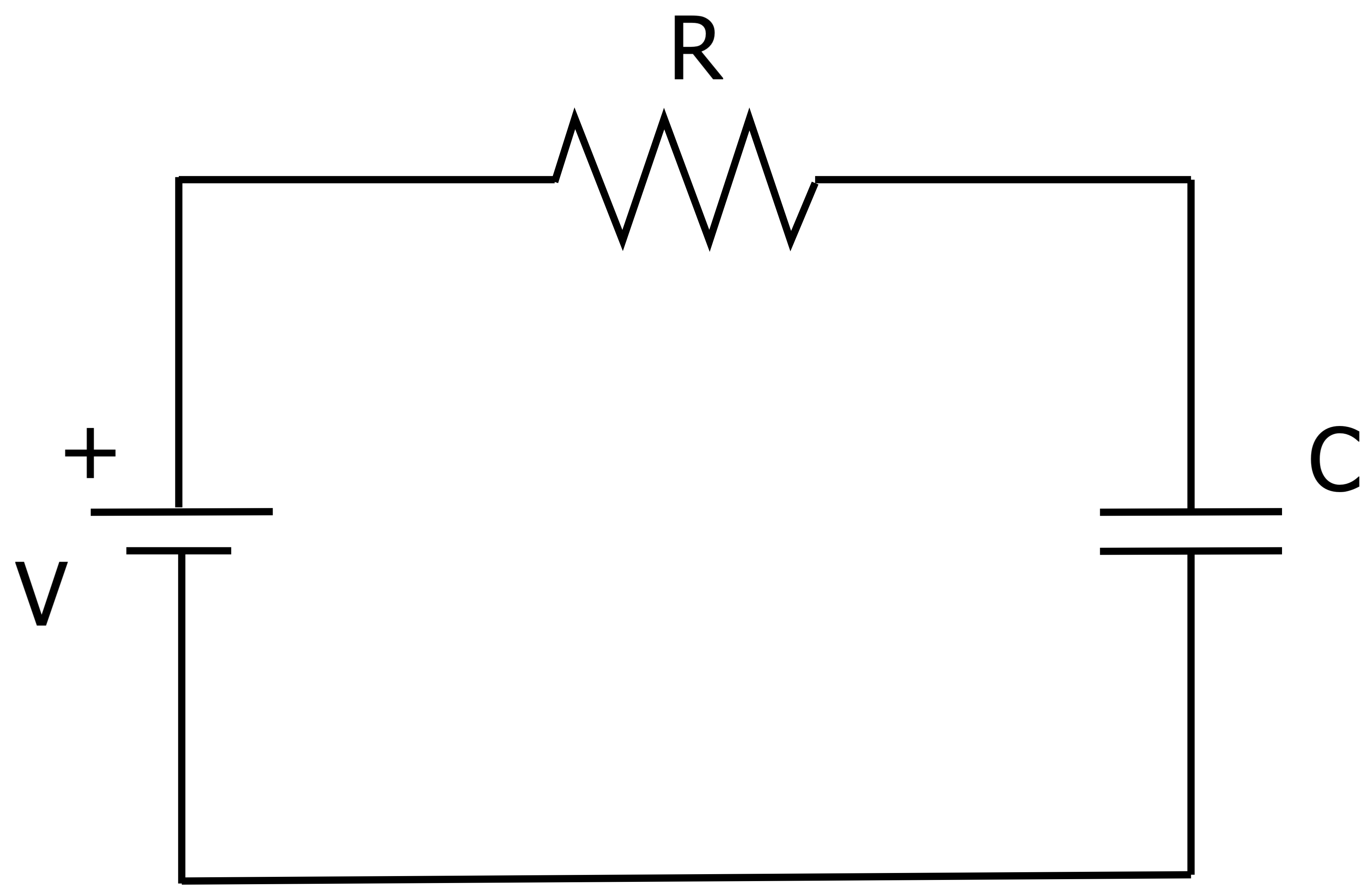
RC Circuit Formulas
RC circuits have several characteristics, including a time constant, energy storage, charge, impedance, capacitive reactance, characteristic frequency, and angular frequency. Calculating each of these characteristics of the circuit can be done using the following formulas.
Time Constant Formula
The time constant, expressed as tau (τ) is the time it takes in seconds for the capacitor in the RC circuit to reach 63.2% charge. The formula to calculate the time constant is:
τ = RC
The time constant τ is equal to the resistance R in ohms times the capacitance C in farads. The capacitor will reach a 63.2% charge in τ, 86.5% in 2τ, and 99.3% in 5τ.
Energy Formula
The energy stored in the fully charged capacitor in an RC circuit can be found using the formula:
E = CV2 / 2
The energy E in joules is equal to the capacitance C in farads times the voltage V squared, divided by two.
Charge Formula
The maximum charge in the resistor capacitor circuit can be found using the formula:
Q = CV
The charge Q in coulombs is equal to the capacitance C in farads times the voltage V.
Current Formula
The maximum current of the RC circuit can be found using Ohm’s Law. The formula is:
I = V / R
The current I in amps is equal to the voltage V divided by the resistance R in ohms.
Characteristic Frequency Formula
The characteristic frequency, often called the ordinary or cyclic frequency, of the circuit can be found using this formula:
f = 1 / 2πRC
The frequency f in hertz is equal to 1 divided by 2 times π times the resistance R in ohms times the capacitance C in farads.
Angular Frequency Formula
The angular frequency of the circuit can be found with the formula:
ω = 2πf
The angular frequency ω in radians per second is equal to 2 times π times the characteristic frequency f in hertz.
Impedance Formula
The impedance of an RC circuit can be found using a few formulas:
Z = R + 1 / jωC
|Z| = √(R2 + 1 / (ωC)2)
Where j is the imaginary unit, Z is the impedance in ohms, R is the resistance in ohms, C is the capacitance in farads, and ω is the angular frequency in rad/s.
Capacitive Reactance Formula
The capacitive reactance of an RC circuit can be found using the formula:
X = 1 / ωC
The capacitive reactance X is equal to 1 divided by the angular frequency ω times the capacitance C.
Phase Difference Formula
This formula expresses the phase difference between total voltage and total current.
φ = tan-1(-1 / ωCR)
φ is the phase difference, ω is the angular frequency, C is the capacitance, and R is the resistance.

