Half-Life Calculator
Calculate half-life, elapsed time, initial, or remaining quantity using this easy calculator. Read below to learn the half-life formula and how to solve it.
Half-Life:
Decay Constant
Mean Lifetime
On this page:
What is Half-Life?
Half-life is the time needed to reduce the quantity of a substance to half its initial amount. It’s is commonly used to define the decay of radioactive material, where half-life is the amount of time needed for half the atoms of a particular isotope to decay.[1]
In the medical world, half-life is also used to describe the time it takes for the concentration of a substance to be reduced to half of the initial dose in your body.[2] This is known as elimination half-life.
How to Calculate Half-Life
You can calculate the amount of substance that will remain after an elapsed time period, given the half-life of the substance and the equation for half-life.
Half-Life Formula
The half-life formula states:
N(t) = N0 × (1 / 2)t/t½
Thus, the remaining quantity N(t) is equal to the initial quantity N0 times 1/2 to the power of the elapsed time t divided by the half-life t½
How to Calculate Time using Radioactive Decay
Using a technique known as carbon dating, it’s possible to estimate the age of an organic compound. This is done by measuring the amount of carbon-14 present in a sample of organic (or previously organic) material and comparing it to the amount that should be present.
Because the half-life of carbon-14 is known to be 5,730 years, we can use the half-life formula to calculate the elapsed time, or age of the material.
Half-Life Formula for Time
By rearranging the half-life formula, we can solve for the amount of time elapsed for an initial quantity to reduce to the remaining quantity.
t = t½ × ln(N(t) ÷ N0) / -ln(2)
The time elapsed t for a substance to be reduced is equal to the half-life t½ times the natural log of the remaining quantity N(t) divided by the initial quantity N0, divided by the negative natural log of 2.
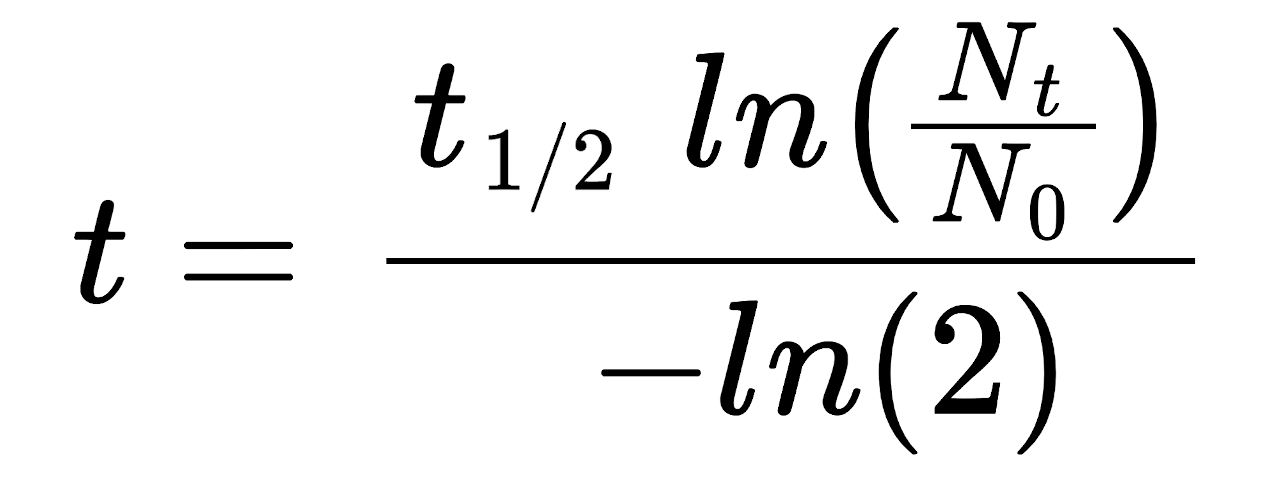
For example, using the formula above let’s use the carbon dating methodology to calculate the age of a sample of organic material that had 15% of the amount of carbon-14 that it should contain if the sample were currently alive. Recall that the half-life of carbon-14 is 5,730 years.
t = 5,730 × ln(15 ÷ 100) / -ln(2)
t = 5,730 × ln(0.15) / -ln(2)
t = 5,730 × -1.897 / -0.693
t = 5,730 × -1.897 / -0.693
t = -10,870.498 / -0.693
t = 15,682.81 years
So, using the half-life formula, we can deduce that this sample is roughly 15,682.81 years old.
Half-Life Decay Table
| Number of Half-Lives | Remaining Quantity (fraction) | Remaining Quantity (decimal) |
|---|---|---|
| 0 | 1 | 1.0 |
| 1 | 1/2 | 0.5 |
| 2 | 1/4 | 0.25 |
| 3 | 1/8 | 0.125 |
| 4 | 1/16 | 0.0625 |
| 5 | 1/32 | 0.03125 |
| 6 | 1/64 | 0.015625 |
| 7 | 1/128 | 0.0078125 |
| 8 | 1/256 | 0.00390625 |
| 9 | 1/512 | 0.001953125 |
| 10 | 1/1,028 | 0.000972762645914 |
You might also be interested in our doubling time calculator.
References
- United States Nuclear Regulatory Committee, Half-life (radiological), https://www.nrc.gov/reading-rm/basic-ref/glossary/half-life-radiological.html
- Hallare J, Gerriets V., Half Life, StatPearls, 2020 Oct 6, https://www.ncbi.nlm.nih.gov/books/NBK554498/