Golden Ratio Calculator
Enter one of the known values to calculate the other values in a golden ratio.
Results:
| Segment (a): | |
| Segment (b): | |
| Sum (a + b): |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Solve the Parts of a Golden Ratio
The golden ratio, also known as the golden section or golden mean, is the ratio between the sum of two values (a + b) to value a being the same as the ratio between value a and value b.
The golden ratio is expressed using the Greek letter φ, or phi.
Thus, the golden ratio can be expressed as:
a + b / a = a / b = φ
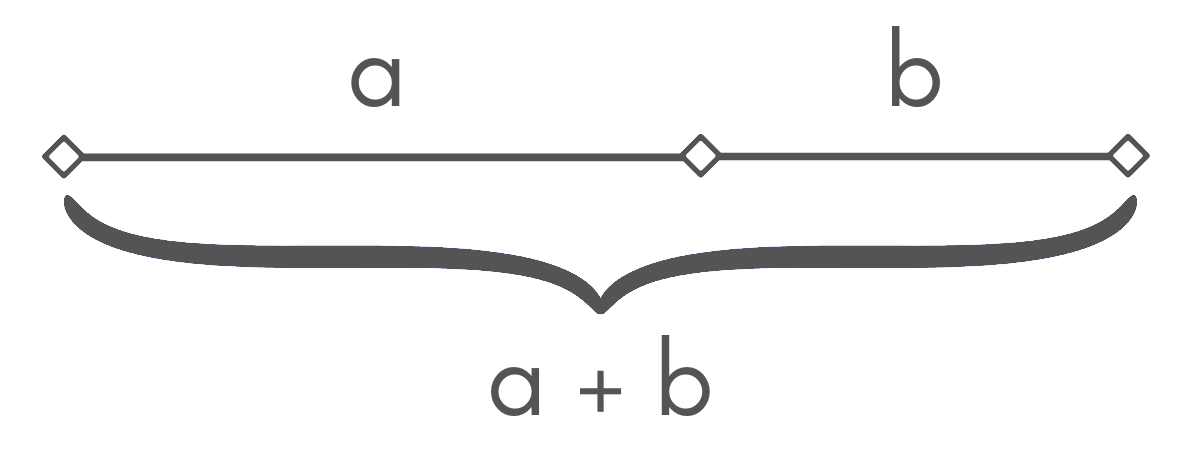
Thus, (a + b) is to a as a is to b. This special ratio is actually derived from the Fibonacci sequence.
The golden ratio can also be expressed using the formula:
φ = 1 + √5 / 2 ≈ 1.618
Thus, the golden ratio φ is equal to 1 plus the square root of 5, divided by 2, or approximately 1.6180327868852. Put more simply, the golden ratio is roughly equal to 1.618.
So, how do you solve values that are part of a golden ratio?
How to Solve for a
If the value b is known, then the following formula can be used to solve for value a if the ratio between them is the golden ratio.
a = b × φ
So, a is equal to b times 1.618.
How to Solve for b
If the value a is known, then the following formula can be used to solve for value b if the ratio between them is the golden ratio.
b = a / φ
So, b is equal to a divided by 1.618.