Vector Subtraction Calculator
Subtract two vectors a and b to find resultant vector a – b using the calculator below.
Vector (a - b):
Steps to Solve
Use the Vector Subtraction Formula
a - b = ({xa - xb}, {ya - yb})
Substitute Values and Solve
Enter vectors a & b above to see the solution here
Steps to Solve
Use the Vector Subtraction Formula
a - b = ({xa - xb}, {ya - yb}, {za - zb})
Substitute Values and Solve
Enter vectors a & b above to see the solution here
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Subtract Vectors
In linear algebra, vectors represent ordered sequences of numbers. You can subtract vectors by subtracting the corresponding components from one another.
The difference of two vectors is referred to as the resultant vector. You can also add vectors using the same technique.
Vector Subtraction Formula
So, the vector subtraction formula looks like this:
a – b = ({xa – xb}, {ya – yb}, {za – zb})
Thus, vector a – b is equal to the difference of the x coordinates of each vector, the difference of the y coordinates of each vector, and the difference of the z coordinates of each vector.
Parallelogram Method
You can also subtract vectors a and b using the parallelogram method.
Using this method, place the two vectors at the same initial point. Then, complete the parallelogram by drawing two additional lines.
Because a negative vector follows the exact opposite direction of the positive vector, you can use the same method as vector addition to solve a vector subtraction problem.
a – b = a + (-b)
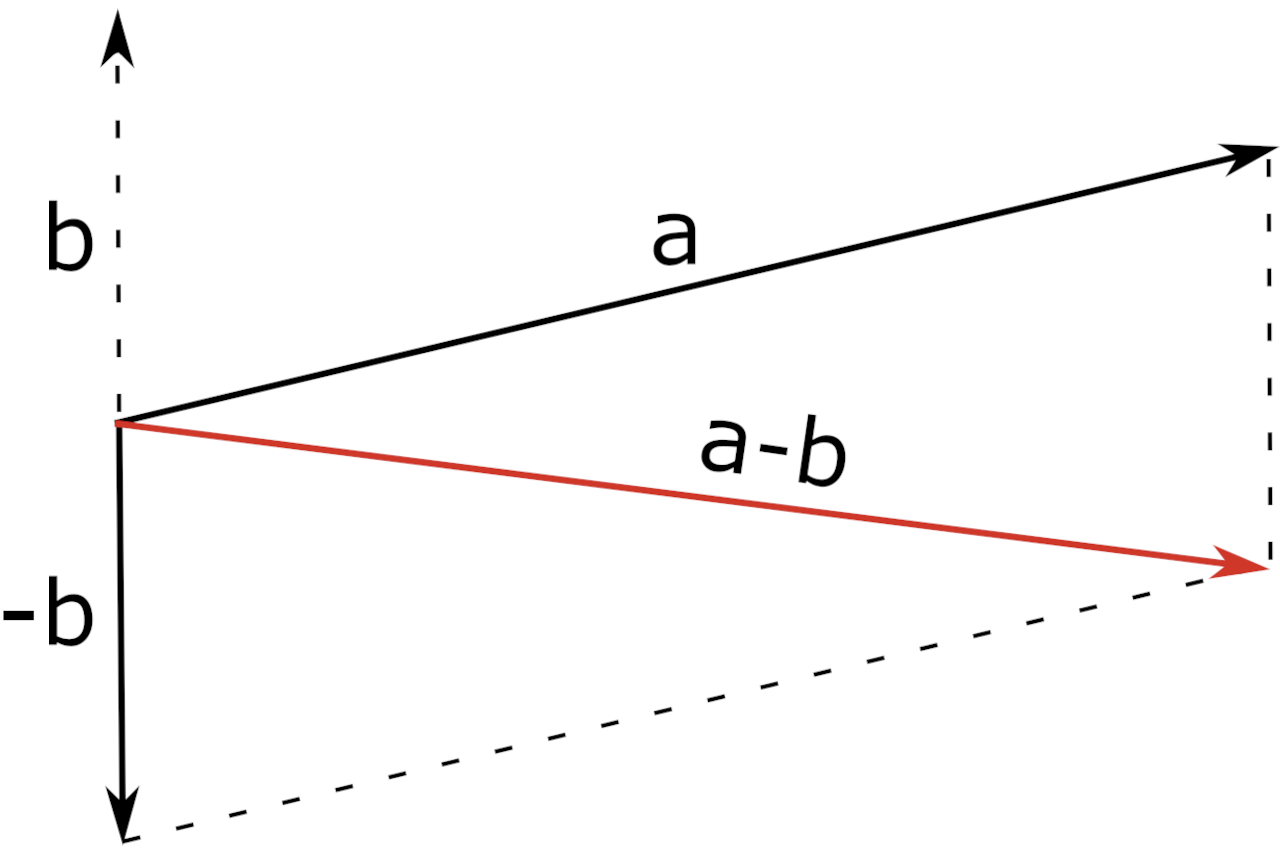
The diagonal of the parallelogram is equal to the resultant vector a – b.
You can also use our cross product calculator or dot product calculator to multiply vectors.