Gravitational Force Calculator
Calculate the gravitational force, the mass of an object, or the distance between objects using the calculator below.
Gravitational Force:
Force Formula
Mass Formula
Distance Formula
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Calculate Gravitational Force
Newton’s Law of Universal Gravitation is a fundamental principle in physics that describes the gravitational attraction between two masses. This law can be used to calculate the force of gravity acting between any two objects.
Newton’s Law of Universal Gravitation
Newton’s Law of Universal Gravitation states that every point mass attracts every other point mass in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This can be expressed mathematically as:
F = Gm1m2 / r²
Where:
F = gravitational force between the two masses
G = gravitational constant
m1 & m2 = masses of the two objects
r = distance between the centers of the two masses
The gravitational force F is equal to the gravitational constant G times the masses of the two objects m1 & m2, divided by the distance between them r squared. This is nearly identical to the calculation for the electrostatic force of two charges defined by Coulomb’s Law.
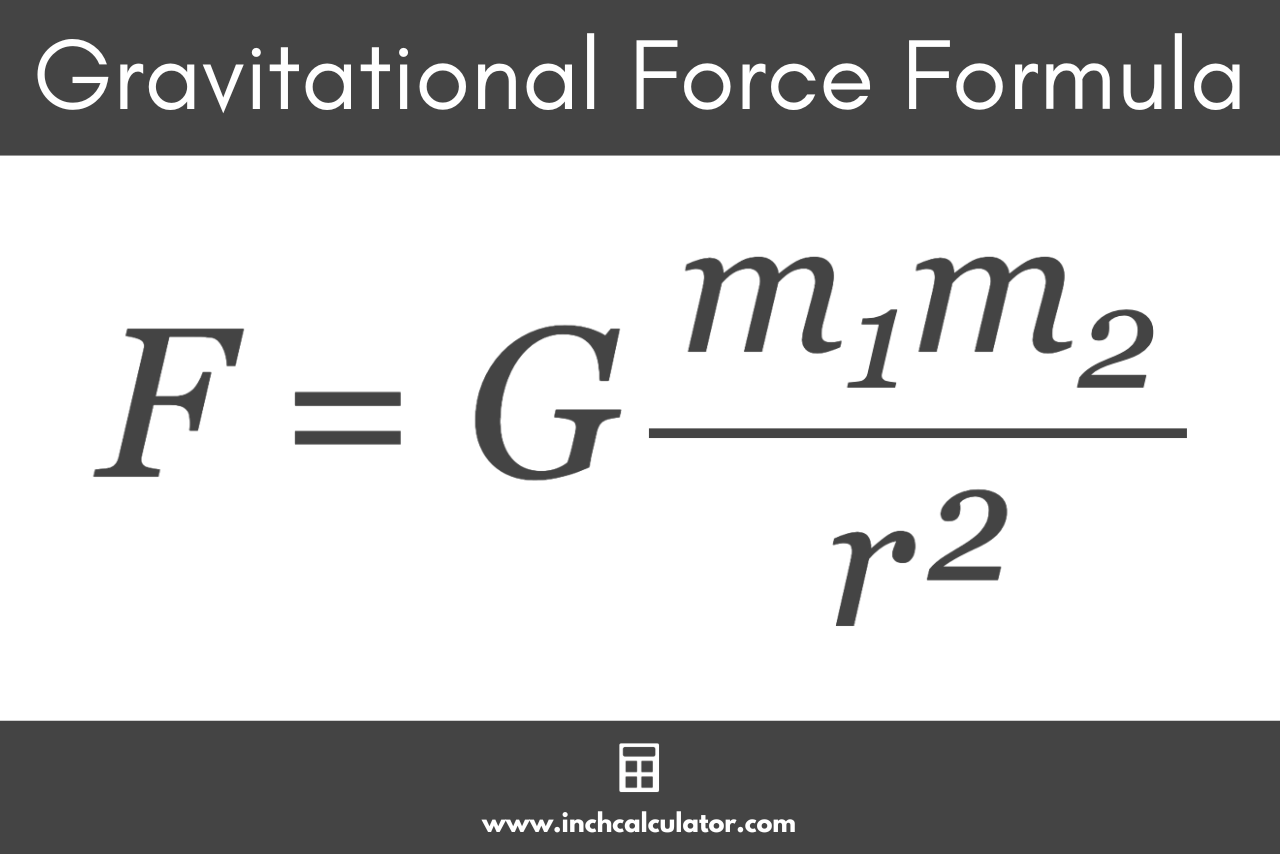
The Gravitational Constant
The gravitational constant G is a key part of the equation, serving as the proportionality factor that makes the equation work across the board. The gravitational constant is approximately equal to 6.674 × 10-11 N(m² /kg²), which is remarkably small.
This indicates that the gravitational force is a weak force, only noticeable when at least one of the objects has a large mass (like a planet).
For example, let’s apply Newton’s Law of Universal Gravitation to calculate the gravitational force between the Earth and an object on its surface. For simplicity, we’ll consider the object to have a mass of 1 kg, and we’ll use the Earth’s average mass of 5.972 × 1024 kg and radius of 6.371 × 106 m.
Substitute the values and the gravitational constant into Newton’s Law of Universal Gravitation.
F = 6.674 × 10-11 N(m² /kg²) · 5.972 × 1024 kg · 1 kg / (6.371 × 106 m)2
Then solve.
F = 6.674 × 10-11 N(m² /kg²) · 5.972 × 1024 kg / (6.371 × 106 m)2
F = 9.8195 N
Thus, the gravitational force between the Earth and a 1 kg object on its surface is approximately 9.82 N. Observe that this is quite close to the acceleration due to gravity (9.81 m/s²), which is what we observe as the “weight” of the object due to Earth’s gravity.