Coulomb’s Law Charge Calculator
Calculate the electrostatic force of attraction/repulsion, distance, or charge using Coulomb’s Law by entering known values in the calculator below.
Calculate Force
Calculate Distance
Calculate Charge
Electrostatic Force:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ahmed holds a Master’s degree in electrical engineering and currently works as an electrical engineer with Energy Systems Research Laboratory.
How to Calculate Electrostatic Force
When two charges are brought together, they experience a force of attraction if they are opposite charges and a force of repulsion if they are like charges. Using Coulomb’s Law it’s possible to calculate the electrostatic force between two charges if the distance between them is known.
Coulomb’s Law Formula
Coulomb’s Law defines the following formula for this.
FE = keq1q2 / r2
Where:
FE = electrostatic force in newtons
ke = Coulomb constant, which is equal to 8,987,551,787.3681764 Nm2C−2 (8.988×109 Nm2C-2)
q1 = charge of the first object in coulombs
q2 = charge of the first object in coulombs
r = distance between the objects in meters
The electrostatic force FE between two charges is equal to the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the distance between them r squared.
Notice that this quite closely resembles Newton’s Law of Universal Gravitation to calculate gravitational force between the masses of two objects.
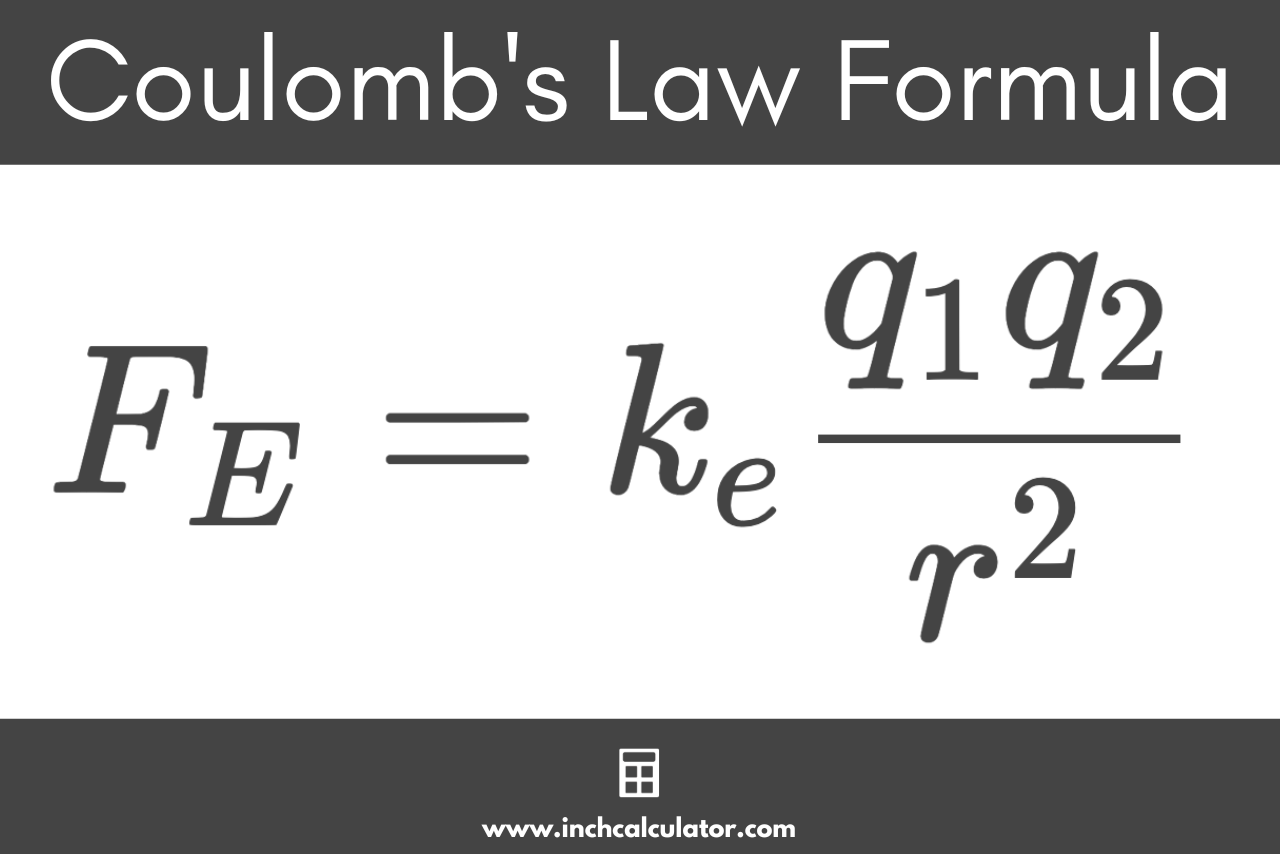
For example, let’s find the electrostatic force between two +2µC and +4µC point charges if a distance of 10 millimeters separates them.
F(N) = (8.988×109 Nm2C-2)(2×10-6 C)(4×10-6 C) / (10×10-3 m)2
F(N) = 719 N
So, the electrostatic force is equal to 719 newtons.
How to Calculate the Distance Between Objects
If the electrostatic charge and force are known, then it’s possible to use Coulomb’s Law to find the distance between the objects.
r = √ (ke × q1 × q2 ÷ FE)
So, the distance between objects r is equal to the square root of the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the electrostatic force FE.
For example, let’s find the separation between two charges, 3µC and 6µC, when a force of 2 N acts between them.
r(m) = √ ((8.988×109 Nm2C-2)(3×10-6 C)(6×10-6 C) ÷ 2 N)
r(m) = 0.288 m
Thus, the distance between the charges is 0.288 meters.
How to Calculate the Charge of an Object
If the electrostatic charge of one object, the force, and the distance are known, then the following formula can be used to solve the charge of the second object.
q2 = FE × r2 ÷ ke ÷ q1
Thus, the charge of an object q
For example, let’s find the charge on an object if the other object has a charge of 8µC, a separation of 5 millimeters, and a force of 10N acts between them.
q2 (nC) = 10 N × (5×10-3 m)2 ÷ 8.988×109 Nm2C-2 ÷ 8×10-6 C
q2 (nC) = 3.5 nC
The charge of the object is equal to 3.5 nC.