Coterminal Angle Calculator
Use our coterminal angle calculator to find the positive and negative coterminal angles for any angle in degrees or radians.
Result:
Positive Coterminal Angles
795°
1,155°
1,515°
1,875°
…
Negative Coterminal Angles
-645°
-1,005°
-1,365°
-1,725°
…
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Find Coterminal Angles
An angle is the measure of the opening between two lines that intersect at a common vertex. Coterminal angles are angles that meet at the same initial and terminal sides.
Coterminal angles will measure the opening between the same two lines revolving around the vertex multiple times. When measured in standard position, coterminal angles always end at the same position.
In standard position, an angle is formed by a rotation originating from the positive x-axis and extending counterclockwise around the origin. This allows angles to be measured consistently.
To better understand coterminal angles, see the diagram below of an angle and the first coterminal angle.
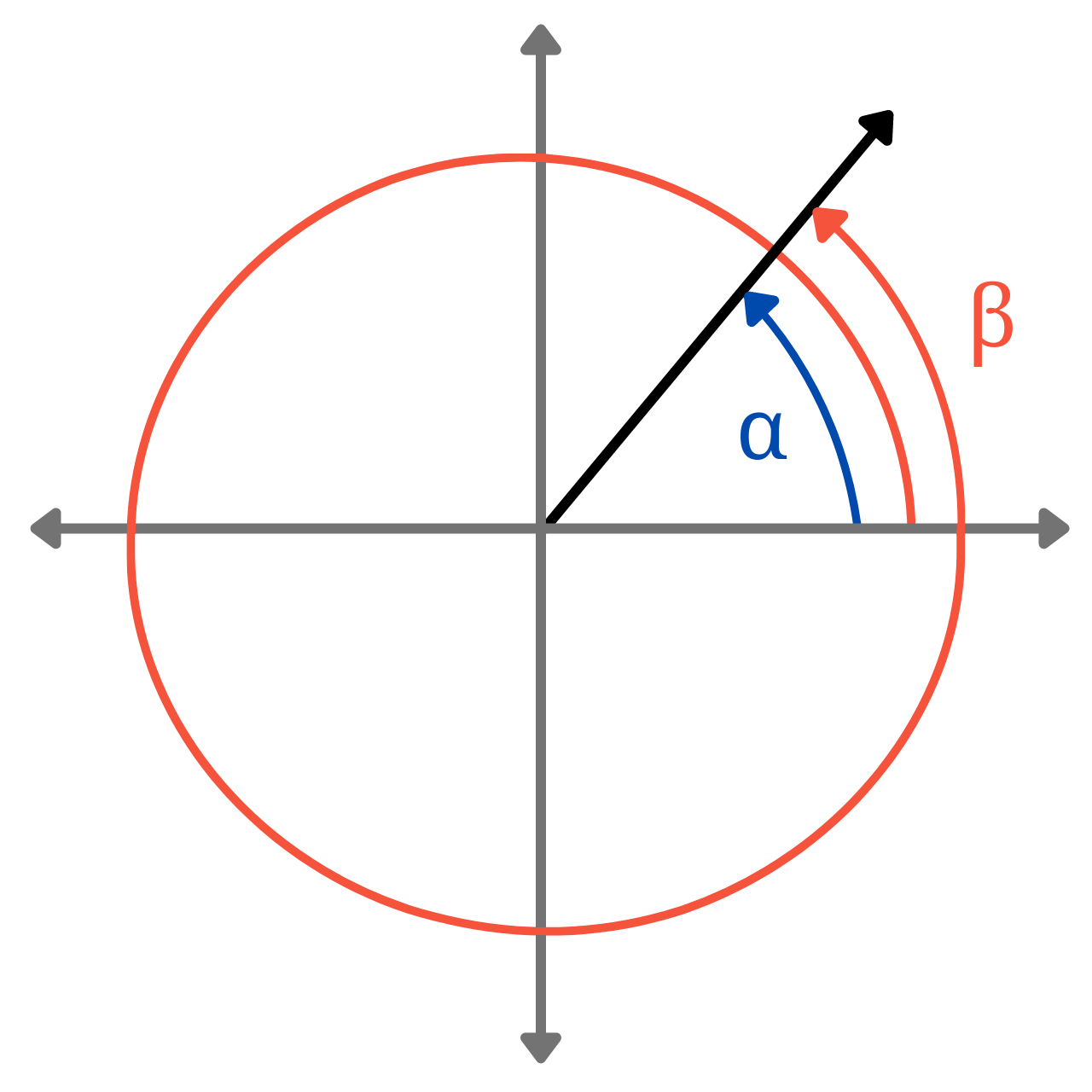
You can find coterminal angles by adding or subtracting multiples of 360 degrees. Since a full rotation is equal to 360 degrees, rotating an additional 360 degrees about a point will arrive at the same position.
For example, let’s find a coterminal angle of 20 degrees.
20 + 360 = 380
By adding 360 to 20 degrees, you’ll find the first coterminal angle of 380 degrees.
This can be expressed using a formula.
Coterminal Angles Formula
You can use the following formulas to find coterminal angles of an angle in degrees or radians.
Coterminal Angles in Degrees:
coterminal angle = θ ± 360n
The coterminal angle is equal to the angle θ in degrees plus or minus 360 times an integer n representing the revolutions about the point.
Coterminal Angles in Radians:
coterminal angle = θ ± 2πn
The coterminal angle is equal to the angle θ in radians plus or minus 2 times pi times an integer n representing the revolutions about the point.
You can also use our degrees to radians converter to allow you to use either formula.
You can apply this formula to find multiple coterminal angles by changing the number n to any whole number.
How to Find Negative Coterminal Angles
Negative coterminal angles are negative angles that start at the standard position and end at the same position as the initial angle. A negative coterminal angle represents a revolution about the point in the opposite direction, as shown in the graphic below.
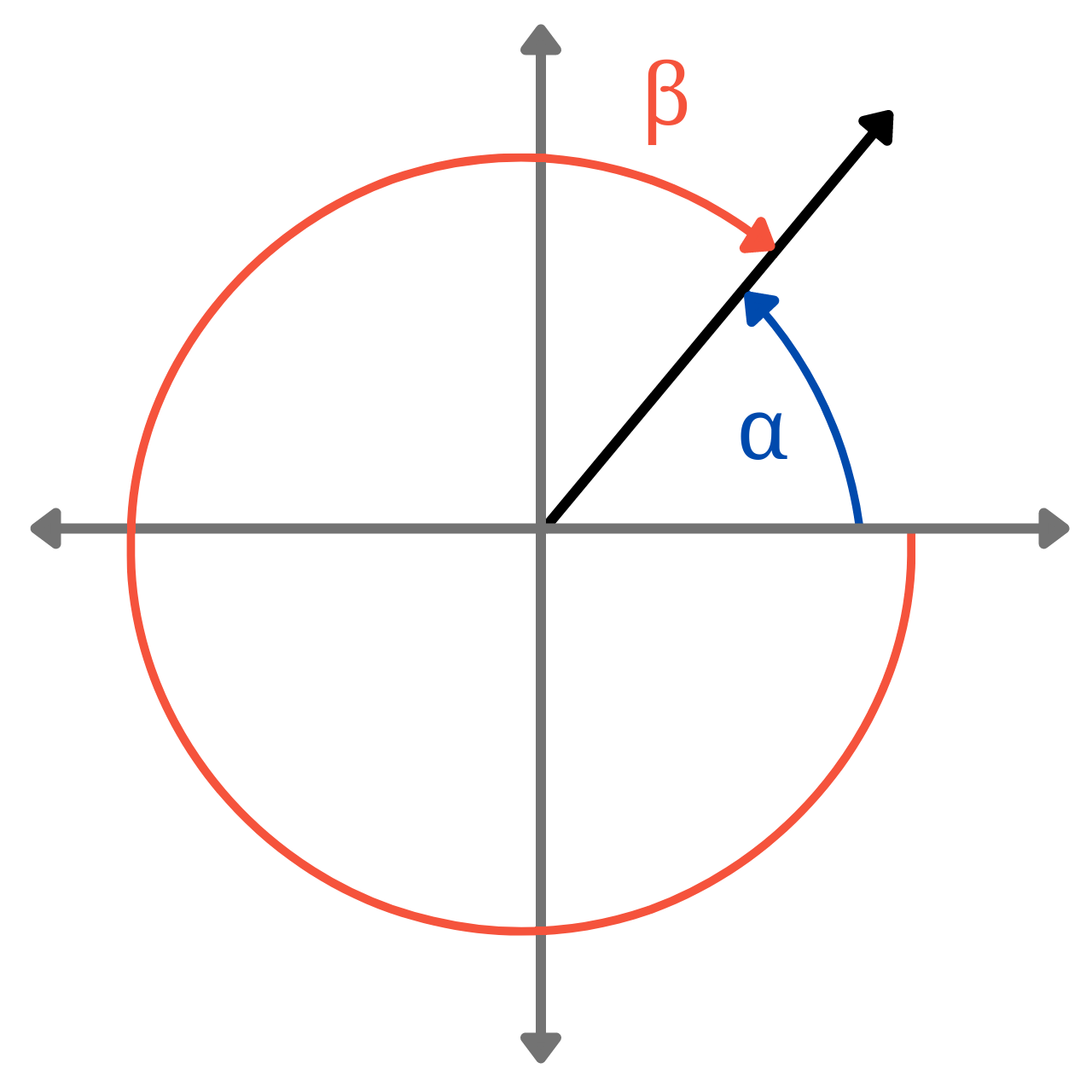
To find a negative coterminal angle, subtract 360 degrees from the angle, which represents one full revolution clockwise, and will arrive at the same position as the angle.
You may also find our reference angle calculator useful for similar trigonometry problems.
Coterminal Angle Chart
| Angle | Positive Coterminal Angle | Negative Coterminal Angle |
|---|---|---|
| 0 | 360 | -360 |
| 10 | 370 | -350 |
| 20 | 380 | -340 |
| 30 | 390 | -330 |
| 40 | 400 | -320 |
| 50 | 410 | -310 |
| 60 | 420 | -300 |
| 70 | 430 | -290 |
| 80 | 440 | -280 |
| 90 | 450 | -270 |
| 100 | 460 | -260 |
| 110 | 470 | -250 |
| 120 | 480 | -240 |
| 130 | 490 | -230 |
| 140 | 500 | -220 |
| 150 | 510 | -210 |
| 160 | 520 | -200 |
| 170 | 530 | -190 |
| 180 | 540 | -180 |
| 190 | 550 | -170 |
| 200 | 560 | -160 |
| 210 | 570 | -150 |
| 220 | 580 | -140 |
| 230 | 590 | -130 |
| 240 | 600 | -120 |
| 250 | 610 | -110 |
| 260 | 620 | -100 |
| 270 | 630 | -90 |
| 280 | 640 | -80 |
| 290 | 650 | -70 |
| 300 | 660 | -60 |
| 310 | 670 | -50 |
| 320 | 680 | -40 |
| 330 | 690 | -30 |
| 340 | 700 | -20 |
| 350 | 710 | -10 |
| 360 | 720 | -360 |
Frequently Asked Questions
Which angles are Coterminal with a 125 degree angle?
The angles that are coterminal with 125° are 485° and -235°.
Why do we use coterminal angles?
Coterminal angles will measure the openings between the same two lines revolving around the vertex multiple times. This helps simplify calculations in geometry and trigonometry.
How do you find a coterminal angle for an angle in radians?
The coterminal angle is equal to the angle θ in radians plus or minus 2 times π times and integer n representing the revolutions about the point.