pH Calculator
Calculate pH using the chemical concentration or mass and volume.
Results:
| pH: | |
| Molar Mass: |
| pH: | |
| Molar Mass: |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Teresa is a chemistry expert with a PhD in environmental science, a Master's degree in earth, atmospheric, and planetary sciences, and Bachelor's degree in chemistry.
What is pH?
pH is a measure of the acidity or alkalinity of a chemical solution. It’s a numerical value expressing how acidic or basic a liquid solution is.
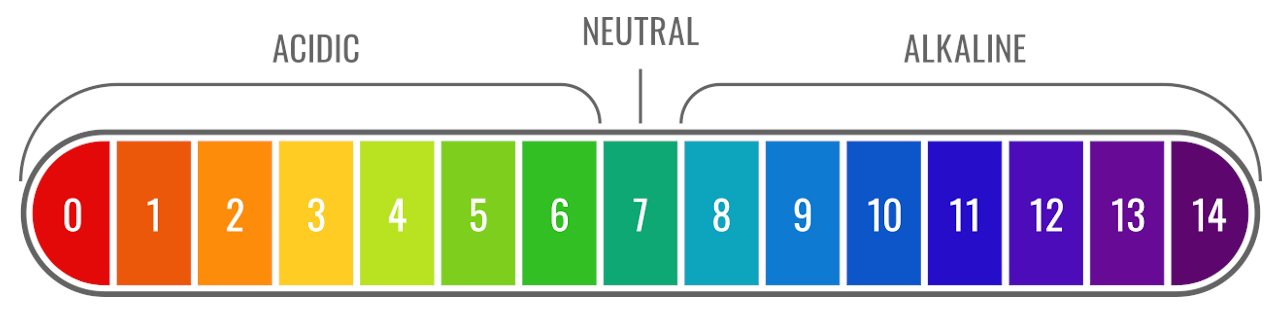
The pH Scale
pH is measured on a scale ranging from 0 to 14. A pH of 7 is considered neutral. Pure water, or an aqueous solution with only neutral chemicals dissolved in it, would have a pH of 7.
Values lower than 7 are acidic, and the lower the pH value, the more acidic the solution is. Values higher than 7 are basic, with higher values being more alkaline.[1]
How to Calculate pH
pH is defined as the negative logarithm of the hydrogen ion concentration.[2] You can calculate pH if you know the molar concentration of hydrogen ions in the solution using a formula.
pH Formula
The formula to find pH is:
pH = −log[H+]
Thus, the pH of a solution is equal to the negative base-10 logarithm of the hydrogen ion concentration [H+]. For example, hydrochloric acid (HCl) is a strong acid that completely dissolves in water to give H+ and Cl–.
For example, let’s calculate the pH of a solution with a hydrogen ion concentration of 0.0000463.
pH = -log(0.0000463)
pH = -(-4.334)
pH = 4.334
This example shows how the pH calculator above works, which can be used to double-check your calculations.
pOH to pH
pOH is a measure of the concentration of hydroxide ions (OH–), and the sum of pH and pOH is always equal to 14. For example, sodium hydroxide (NaOH) is a strong base that completely dissolves in water to give Na+ and OH–.
pH + pOH = 14
Thus, you can calculate pH if you know this value using the following formula:
pH = 14 – pOH
You can also calculate pOH in the same manner:
pOH = 14 – pH
As you can see from these formulas, the higher the concentration of hydrogen ions, the lower the pH will be, and the more acidic the solution will be. On the other hand, the higher the concentration of hydroxide ions, the higher the pH will be, and the more basic or alkaline the solution will be.
How to Calculate H+
If you know the pH of a solution, you can find the hydrogen concentration by reversing the sides in the formula above.
pH to H+ Formula
So, the pH to [H+] formula is:
[H+] = 10-pH
The hydrogen ion concentration [H+] is equal to 10 to the power of the negative pH value.
How to Find pH from Molarity
The molarity of a solution is equal to the hydrogen concentration [H+] in moles per liter. Given this, you can find the pH of a solution using the molarity with the formula above.
pH = −log[H+]
pH is equal to the negative base-10 logarithm of the molarity of the solution, which is the hydrogen ion concentration [H+].
How to Find the pH of Strong Acids and Bases
Strong acids and bases dissolve completely into water, releasing all of their hydrogen and hydroxide ions. For a strong acid, the hydrogen ion concentration will be equal to the number of hydrogens in the original acid, multiplied by the molarity (mol/L) of the acid.
For example, for hydrochloric acid, the chemical reaction is:
HCl (aq) = H+ (aq) + Cl– (aq)
The notation (aq) means the reaction is aqueous, or taking place in water. Like most strong acids, HCl releases one H+ ion, and is known as a “monoprotic” acid.
Therefore, the [H+] is equal to the original molarity of the acid.
However, some strong acids have more than one hydrogen. For example, sulfuric acid, H2SO4, has two hydrogens that each dissociate completely in water:
H2SO4 (aq) = 2H+ (aq) + SO42– (aq)
Because each mole of H2SO4 releases 2 moles of H+, the [H+] will be double that of a strong acid with only one H+. Acids that release more than one H+ are known as “polyprotic.”
Going back to our original example, the pH of a solution of HCl in water with an [H+] of 0.0000463 is 4.334. The same concentration of H2SO4 would release twice as much H+:
[H+] = 2 × 0.0000463 = 0.0000926
The pH is calculated in the same manner as before:
pH = −log[H+]
pH = -log(0.0000926)
pH = -(-4.03)
pH = 4.03
Therefore, we can see that strong acids that release more than one hydrogen result in a more acidic solution than acids that release only one hydrogen.
The same relationship holds true for bases – strong bases that release more than one hydroxide ion result in a more alkaline solution than bases that release only one hydroxide ion.
How to Find the pH of Weak Acids and Bases
Most acids and bases do not dissolve completely in solution – these are called “weak” acids and bases. Finding the pH of these solutions is more complicated than for strong acids and bases because they each ionize to different degrees.
To find the pH of a solution of a weak acid or base, you will use a “dissociation constant,” Ka for acids and Kb for bases. The larger the value of K, the stronger the acid or base and the more it goes into the solution.
K is also called the “equilibrium constant” for general chemical reactions, and represents the concentrations of the products over the concentrations of the reactants in the solution.
Recall that acids release hydrogen ions, which make the solution more acidic and lower the pH. Ka represents the proportion of hydrogen ion that is released vs. the amount that stays attached to the original chemical.
In the equation below, [H+] is the hydrogen ion concentration, [A–] is the concentration of the acid without the hydrogen ion, and [HA] is the amount of the original weak acid that has not dissociated:
Ka = [H+] × [A–] ÷ [HA]
From this equation, you can see that the more of the acid that dissociates, the higher Ka will be and the larger the [H+] concentration. We can rearrange this equation to solve for [H+] and calculate the pH of this solution if we know the acid dissociation constant and the original concentration of the solution.
Let’s start rearranging the above equation:
[H+] × [A–] = Ka × [HA]
In this equation, the concentration of the positively charged hydrogen ion and the negatively charged acid ion will be the same. Therefore, [H+] = [A–], and we can rewrite this as:
[H+]2 = Ka × [HA]
or
[H+] = (Ka × [HA])½
Since pH = -log[H+], we can then calculate pH as:
pH = -log(Ka × [HA])½
Where Ka is the dissociation constant for the acid and HA is the initial molar concentration.
References
- United States Geological Survey, pH and Water, https://www.usgs.gov/special-topics/water-science-school/science/ph-and-water
- Determining and Calculating pH, 2020, August 15, https://chem.libretexts.org/@go/page/1292