Parallel Resistor Calculator
Calculate the total resistance in ohms of resistors that are in parallel by entering the value of each below.
Parallel Resistance:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ahmed holds a Master’s degree in electrical engineering and currently works as an electrical engineer with Energy Systems Research Laboratory.
Do you want to calculate resistors in series?
How to Calculate Parallel Resistance
A resistor is a device that adds resistance to an electrical circuit. Resistance is measured in ohms (Ω), and that’s also the measure used by this calculator.
Resistance is the inherent property of conductors, materials, and devices to oppose the flow of charge through them. A lower resistive value means that the material is more conductive, and a higher value means that the material has a stronger insulating property.
It is measured in its standard unit of ohm; one ohm equals the resistance of a conductor through which a current of one ampere flows when a potential difference of one volt is applied to it.
When resistors are connected in series, the resistance values add up because the same current flows through them.
However, when resistors are added in parallel in a circuit, they are connected to the same points as each other, thus there are multiple paths that voltage can take. Because of this, the reciprocal of each resistance value must be added together to find the total resistance of the circuit.
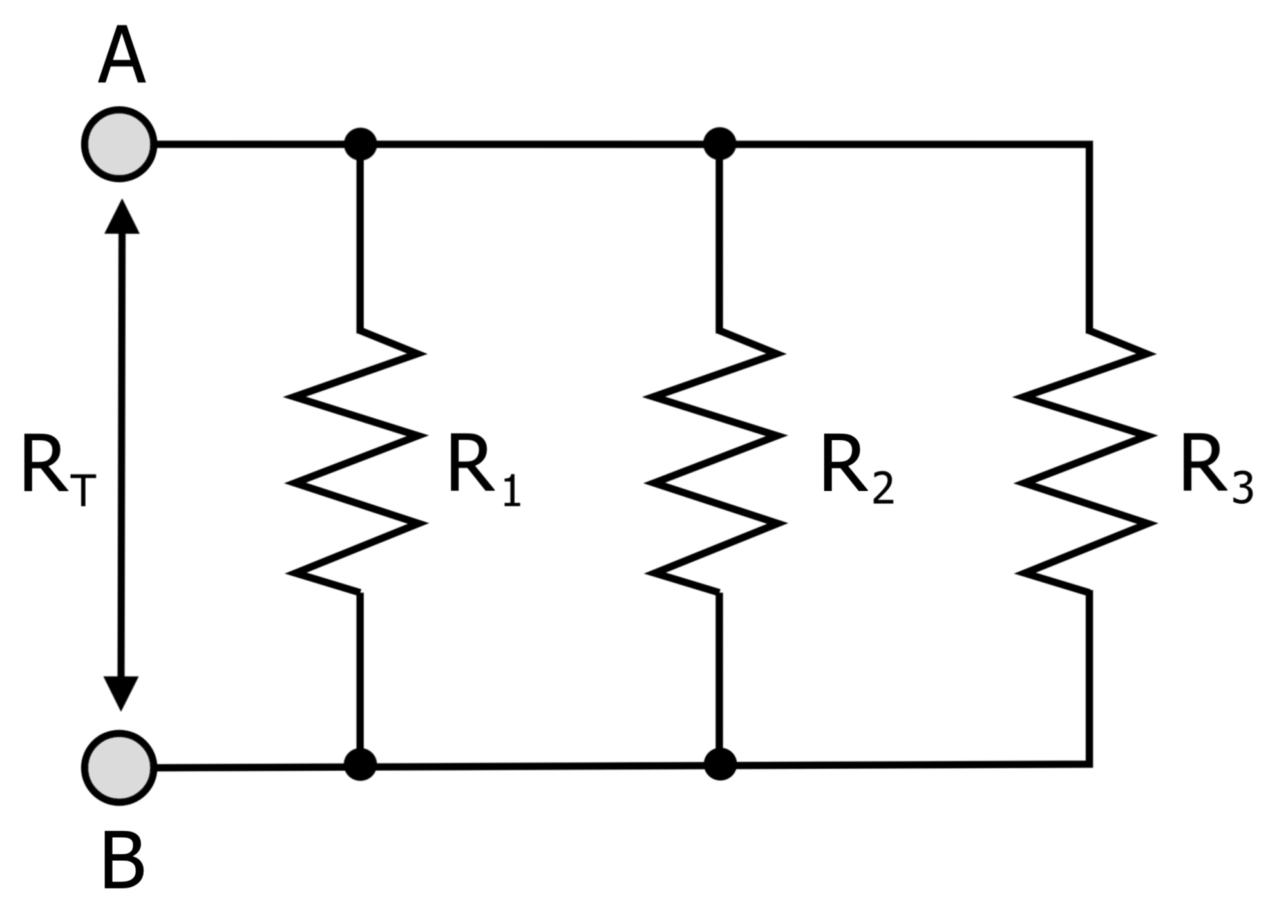
Each parallel resistor has the same voltage value across its common terminals. This fact is used for house wiring because the different loads (resistances) are connected to the same power source.
When they are all switched on, they all have the same supply voltage across their terminals, but each provides a separate path to current, reducing the overall resistance of the connected loads.[1]
Parallel Resistor Formula
When multiple resistors are added to a circuit in parallel the total resistance can be found using this formula.
1 / RT = 1 / R1 + 1 / R2 + … + 1 / Rn
Thus, the reciprocal of the total resistance of resistors connected in parallel is the sum of the reciprocal of each resistance.[2]
For example, let’s find the total resistance of a circuit with 200 Ω, 400 Ω, and 500 Ω resistors connected in parallel.
1 / RT = 1 / 200 Ω + 1 / 400 Ω + 1 / 500 Ω
1 / RT = 0.005 + 0.0025 + 0.002
1 / RT = 0.0095
RT = 1 ÷ 0.0095
RT = 105.263 Ω
If several resistors of the same value are connected in parallel, then the total resistance can be found by dividing the common resistance value by the number of resistors connected in parallel.
For example, let’s say we have two 4 Ω resistors, each connected in parallel. The equivalent resistance according to the above equation becomes:
1 / RT = 1 / 4 Ω + 1 / 4 Ω
1 / RT = 2 / 4
RT = 4 / 2
RT = 2 Ω
We can generally rewrite the formula for n number of equal parallel resistors as:
1 / RT = n / R
Using this new formula on the above example, we get:
1 / RT = 2 / 4
RT = 4 / 2
RT = 2 Ω
References
- LibreTexts - Physics, College Physics (OpenStax) - 21.1: Resistors in Series and Parallel, https://phys.libretexts.org/Bookshelves/College_Physics/Book%3A_College_Physics_1e_(OpenStax)/21%3A_Circuits_Bioelectricity_and_DC_Instruments/21.01%3A_Resistors_in_Series_and_Parallel
- Electronics Hub, Resistors in Parallel, https://www.electronicshub.org/resistors-in-parallel/